Add setting to select type of insulin A) Novo/Humalog B) FIAsp

If A selected use current curve calculation If B selected use maths to match curve as described on page 12 of http://www.ema.europa.eu/docs/en_GB/document_library/EPAR_-_Product_Information/human/004046/WC500220890.pdf

Integral-retrospective-correction or IRC is an experimental modification of the Loop's Retrospective Correction.

Integral Retrospective Correction (IRC) Status (Nov. 2019):

• IRC is not a standard Loop feature and is not considered for inclusion in the standard Loop at this time.
• IRC is considered highly experimental and is not recommended for new Loop users or users who are having issues with Loop settings.
• The IRC algorithm was developed and implemented during 2018. At this time, the IRC algorithm and the IRC code are stable, and there are no known bugs.
• Until further notice, I am planning to keep the IRC branch closely up to date with Loop dev branch for my own personal use. Since the Loop dev branch is updated very often, the IRC branch may be behind Loop dev at times.
• If you wish to try IRC, you may do so on your own following the standard Loop installation directions. Please do not distribute IRC to other Loop users in any form.
• Feel free to contact me (@ Dragan Maksimovic on Loop Zulip) about any algorithm questions or feedback you may have about IRC, but please note that I am unable to provide any installation support or any other technical support.
• In the IRC branch, the IRC feature is disabled by default, and standard RC is enabled. To enable IRC, tap on the glucose chart, scroll down to the Algorithm Settings and turn the slider switch on.

1. Known risk factors compared to standard Loop: with IRC turned on, in response to persistent discrepancies between observed and predicted glucose motion, Loop may increase insulin corrections, which may increase risks of hypoglycemia. In general, IRC may also lead to increased oscillations ("roller-coaster") in glucose responses. Both of these risk factors are increased if the user's setting value for Insulin Sensitivity (ISF) is too low. Increasing ISF setting value tends to mitigate these risks but it is impossible to offer any guarantees for anything around your own T1D.

2. Compared to standard Loop, IRC is more likely to improve glucose control in the following situations:

• Glucose staying above (or below) the correction range due to too low (or too high) basal rate settings
• Glucose spikes (or dips) on tail ends of meals where carbs entered are underestimated or overestimated
• Glucose spikes due to unannounced protein+fat effects
• Glucose spikes due to any unannounced meals

The current implementation of the IRC code is in IntegralRetrospectiveCorrection.swift and the algorithm is described below.

******************** .IRC Algorithm Description ******************************************** Integral retrospective correction (integral RC) is an experimental modification of the Loop's retrospective correction algorithm. Loop with integral RC, which is based on the current dev branch of Loop, has no customization other than the IRC code. Just as the standard RC, the motivation behind integral RC is to make Loop less dependent on how well carb entries, ISF, CR, or programmed basal rates represent reality, and to improve responses in the presence of any unmodeled factors.

If you are interested in trying out the experimental integral RC Loop branch, some points to note:

• I believe the algorithm and the code are safe and suitable for testing purposes, but since Loop with integral RC is even more highly experimental than standard Loop please do not even consider trying unless you are a Loop user who is willing and able to carefully observe operation and provide feedback. There are measures takes so that IRC should not make anything worse, but there is no way to guarantee that. Too low ISF setting value may lead to increased risks of hypoglycemia or oscillatory glucose responses.
• Please do not expect any immediate or very substantial improvements. The algorithm changes described here are relatively modest tweaks to existing Loop algorithms.
• Please read through the rest of this post (which is rather long, sorry), and feel free to ask any questions.

Integral retrospective correction: algorithm description

Operation of the standard Loop retrospective correction is illustrated below, where time = 0 represents present time.
A modeling error called discrepancy is calculated as the difference between the actual BG and the BG predicted based on insulin and carbs models over the past 30 minutes. In the example shown, discrepancy = 15 mg/dL. The discrepancy is then used to modify the BG forecast over a correction interval of 60 min. The net effect of standard RC is that the eventual predicted BG is adjusted up (or down) by a retrospective correction equal to the current discrepancy (subject to momentum effects, but that’s a different topic).

In the integral RC, the correction magnitude and the correction time interval depend not only on the current discrepancy but also on past discrepancy values, so that the correction becomes more aggressive if discrepancy persists over consecutive Loop cycles. This results is more aggressive dosing in response to any persistent modeling errors due to over/under-estimated carbs, parameters (ISF, CR, or basal rates) being away from reality, exercise, … whatever.

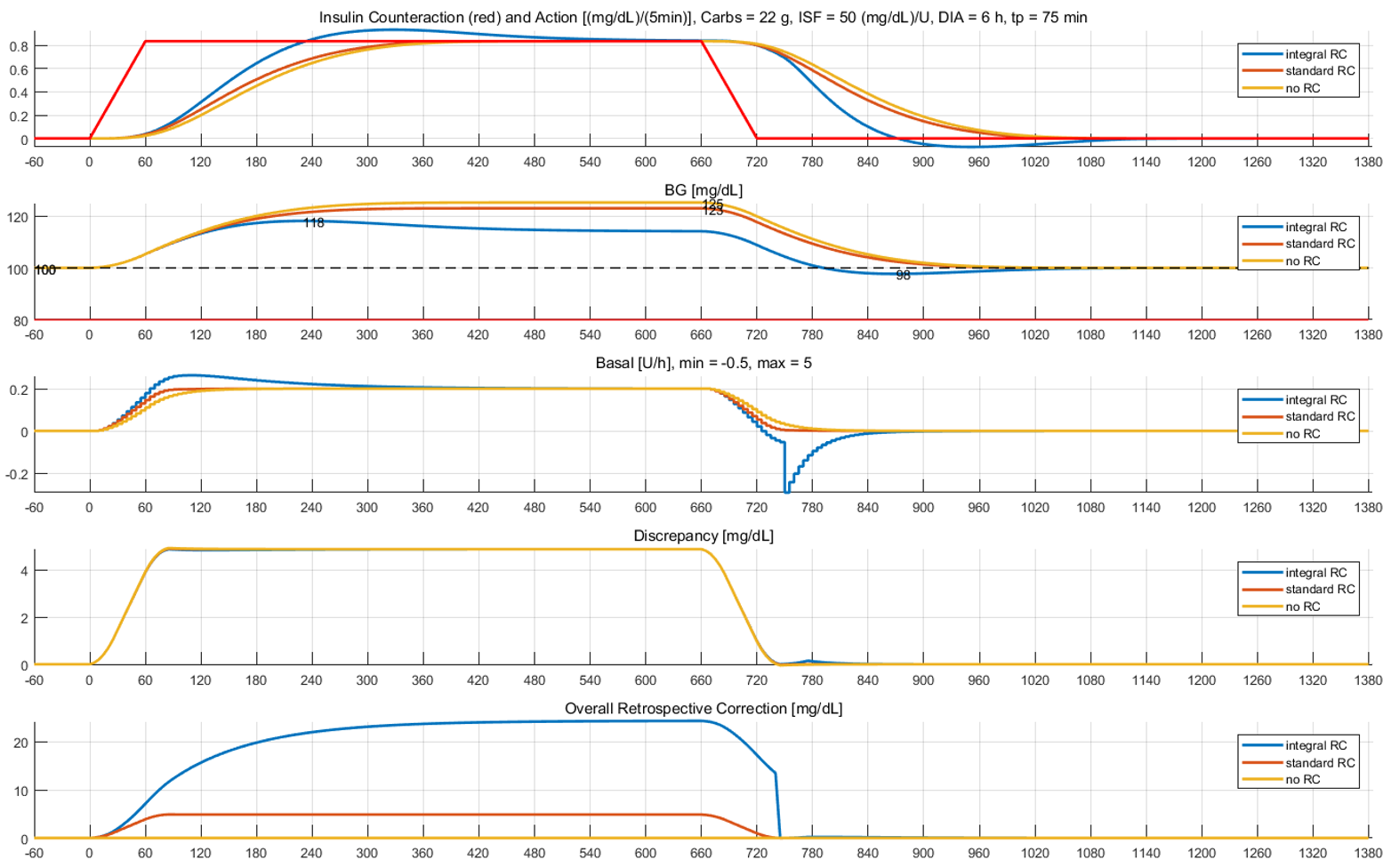
Simulation examples

In the first example, the actual basal needs increase by 40% (to 0.7 U/h) over a period of about 10 hours. Standard Loop high temps, which keeps BG from ramping up, but BG hovers away from the target. Integral RC kicks in more aggressive high temp corrections, which brings BG closer to the target.

In the second simulation example, the actual basal needs fall by 40% (to 0.3 U/h) over a period of around 10 hours. Standard Loop responds by low temping, but BG still drops below suspend threshold, which triggers some on/off oscillations around the suspend threshold. Integral RC results in a smaller BG drop and keeps BG closer to the target throughout.

The third example is a case of unannounced 25 g carbs with absorption time of about 3 hours. Compared to the standard Loop, integral RC reduces the magnitude and the duration of the spike.

Integral RC math

Integral RC math is relatively simple. Overall retrospective correction is computed as a sum of two components, proportional and integral:

overallDiscrepancy = proportionalGain * discrepancy + integralDiscrepancy

where integralDiscrepancy is computed as:

integralDiscrepancy = integralForget * integralDiscrepancy + integralGain * discrepancy

proportionalGain, integralForget and integralGain are constant parameters of the integral RC filter. In the standard RC, proportionalGain = 1, and integralGain = 0. In simple control theory terms, standard RC can be viewed as a proportional (P) controller trying to reduce modeling error (discrepancy). Integral RC adds an integral (I) action to this control loop. In addition to the above basic math, safety provisions (integration resets and limits) are included to minimize chances of over-correction.

Discussed a little bit here where Loop shows Missing data: Glucose data not available, though the Dexcom app shows no gaps and appears to otherwise be functioning fine.

It is mentioned by @Kdisimone in the thread that this may be due to an iOS resource issue, but I was hoping there would be a way to make Loop reconnect? Someone else suggested that it's due to Apple Health lagging, but it never seemed to catch up in my case.

Looking back, Apple Health has no Glucose measurements from Loop during that time, but Dexcom shows no interruptions. I can get back into a working Loop state when it happens by toggling Bluetooth on and off.

I have set up Amplitude so I'll have that if it happens again in the future, but is there anything else I could do to help narrow down where the issue may be?

I’m using Dexcom G5 and Dexcom app and have seen the issue on Loop 1.9.2.

An implementation of using boluses for dosing. Independent of https://github.com/LoopKit/Loop/pull/1205.

This feature is enabled by a new switch in settings that allows the user to select between the existing temp basal strategy and this new bolus strategy.

Boluses are issued for high corrections, when Loop thinks additional insulin is required beyond your basal needs. During each loop, up to 40% of the required insulin will be dosed via bolus. When insulin requirements are below basal, Loop will use temp basals, as before. High temps are no longer used, except to maintain scaled basal when a high override is in effect.

Automatic bolus sizes are limited to not exceed 40% of your max bolus setting.

Yesterday I mountain biked for 4:20:00 in 92 degree weather, I once did a Marathon, and I have done 100+ mile road bike rides-so I get to use activity modes a lot. With a plain pump, I can do great simply by turning basal to 15-20% my normal rate. If I don't do this, I must eat about 30 grams of carb an hour, and that also works, but sometimes I just don't feel like eating/drinking or carrying so much food.

With OpenAPS and Loop, I set an activity-mode target to about 140. Problem is, those modes have never really worked for me unless I eat / drink non-stop. Yesterday for my 4:20 of riding, I had to eat 14 cookies to keep from going low during the ride. That amounts to one Oreo cookie every 20 minutes, or about 30 grams of carb per hour - the same as if I had a pump and did nothing to the settings. So while the activity mode gave me some extra margin of safety, it never really addressed the root problem.

My idea is for Loop to have a new configuration setting where you tell it what percentage of normal basal you want for when activity mode is active. It should accept a value from 0-100%, and I will set mine to 20%. It then reduces basal to this whenever activity mode is on.

Hi, I have a lot of problems with rileylink signals, the problem is that lot of time the signal is close to -99db or less and then is not connecting. of course when I'm at home is easy to find some static position with a good signal, but when my son is out of home is difficult to control it.

He is wearing a belt to assure the pump and the rileylink are close and in transversal position ( the pump horizontal and the riley vertical).

The system turn Green after few minutes, so in the stable Bg is not a problem, but with a big bg changes the proposed temp could be important.

know anybody how to improve the connection signal?

thanks

I am using a medtronic 715wws pump. I am using offline-mode only with dexcom share.

Loop 1.4 no problems. Loop 1.5: boluses fail every time with the attached error message

The pump actually successfully enacts the bolus every time, despite this error message. 20 minutes after, the loop sends a notification that loop hasn't run successfully in 20 minutes and the loop circle is red.

Here's the output from xcode terminal while running a bolus: https://gist.github.com/dabear/eab8ac4b982307e44167fc97c3a6f9a6

I have noticed that my carb entries disappear sometimes. This happened most recently during the evening of 4/23/2018. It happened again on the morning of 4/24/2018.

During the evening of 4/23/2018, I entered 40g CHO for supper. It disappeared. Loop predicted a low, given that I had bolused for the meal already. I re-entered the carbs. The carbs showed up twice in Nightscout. They disappeared from Loop again. This happened several more times throughout the evening. Loop would predict significant highs (over 300 or over 500) and significant lows (negative values). I had to open the loop for the night, as I wasn't confident in Loop at all for managing my BG overnight. I captured numerous screenshots. The issue report was captured some time after the initial disappearance.

During the morning of 4/24/2018, I entered 37g CHO for breakfast. It disappeared again. Loop predicted a low again. I re-entered the carbs, and it "stuck" this time. Again, Nightscout showed two entries for the same number of carbs. I captured the issue report soon after the carbs disappeared.

FILES from 4/23/2018 Loop.Disappearing Carb Entries.20180423.pdf

FILES from 4/24/2018 Loop.Disappearing Carb Entries.20180424.pdf

rsilvers FPU modifications.

Adds in support for fat and protein.

See Wiki:

https://github.com/rsilvers129/Loop/wiki/Fat-Protein-Unit-Branch-(FPU-dev)-of-Loop!-With-IRC-and-Spike.

See video:

https://www.youtube.com/watch?v=OvpRUlD0acU

Many (dozens, as found in history of Gitter channel) of users have expressed a desire to have the Loop bolus wizard pop up with a suggested bolus even if their current BG is below the bottom of the Target Range. Users indicate their desire to bolus in preparation for an upcoming meal, even if their BG is below that target as long as they are not "low". Different users have different values to what they consider to be "low".

The concept is to add an an optional setting that allows the user to enter BG value to indicate their preference. Single field entry for BG (in preferred units as determined by which unit value is used in BG in Apple Health)

• If the lower of currently or any future predicted BG is at or below entered value, then do not suggest a bolus
• If the lower of currently or any future predicted BG is above the entered value, then attempt to recommend a bolus and display to the user if one is in fact suggested
• If no value is given by the user, then use the bottom of the Target Range (as it works today).

As to not add additional entries to an already long list under Settings, this could live under the Maximum bolus setting.

If the community supports this feature design, I will code up and submit a PR.

This is inspired in part by the discussion in #388 where @ps2 and others noted that longer-tail exponential insulin absorption curves may expose some shortcomings of the dosing calculation, which is currently based on BG predicted at t=DIA in the future. Currently, the amount of bolus insulin suggested after a meal is entered is found as follows: Such DIA-based dosing works well in many cases. However, it ignores the effect of the insulin delivered on BG between now (t=0) and DIA, which may result in too high or too low amount suggested. To address this issue, one may consider an iterative dosing algorithm that would search for an insulin dose so that BG predicted after the dose is delivered does not go below a target. Such iteration can in fact be captured by a relatively simple modification of the above dosing calculation: The argument of the min function has the meaning of the amount of insulin required to drive BG to the target value at time t. The 1-IOB(t) term in the denominator represents the fraction of to-be-dosed insulin expended from 0 to time t. By choosing the minimum of the doses suggested over the time interval from t=0 to t=DIA we guarantee that the predicted BG, after the dose is delivered, will just touch the target value BGtarget at some point in time between now and DIA (not necessarily at DIA).

To illustrate how the suggested dynamic dosing calculation would work, consider a simple scenario: ISF=50, CR=10, DIA=6 hours, and meal of 50g that absorbs slowly at constant rate over a period of 5 hours. Since the entire meal is absorbed within DIA, the current dosing calculation would suggest 50/10 = 5 U bolus. A simple simulation shown below indicates that this dose is too large for the given meal, with BG dropping from initial 100 mg/dL to as low as 56 mg/dL (neglecting any low temping, which is not simulated here, but which would be insufficient to prevent the low) In the same example, the dynamic dosing suggests 3.7 U, and the simulation shows that BG just touches the target (100 mg/dL) back at around 200min, which is t=140min after the dose is delivered. Since this initial dose is insufficient to cover all carbs, BG eventually drifts up to a value above the target, but this would be corrected by Loop high-temping (which is not included in this simple calculation).

I think the suggested modification of the dosing algorithm could apply to both boluses and temps, and I think everything necessary to perform the calculation is available in DoseMath.

A concern is that the dynamic dosing described above may be too conservative, especially in view of the Loop dynamic carb absorption algorithm, which includes a 50% extension to a user-entered carb absorption time. The dynamic dosing formula could be modified to be more aggressive in at least two ways: by replacing BGtarget with BGmin (or perhaps even BGguard just for boluses), or by taking into account the effect future zero temping could have on predicted BG, thus enabling sort of dynamic super-bolusing as a part of the algorithm. The formula below includes both of these modifications:

Describe the bug Loop projected an Eventual -456 mg/dl glucose level, and the math didn't make sense for parameters, IOB, COB, etc. Loop shut off insulin delivery due to this. Please see the screenshots and files for more details. Enter the new Commit on Dec 31, 2022, yesterday morning, and it worked fine before this.

To Reproduce Steps to reproduce the behavior:

1. Had Custom Preset on for morning workout
2. Changed Custom Preset off and entered carbs for morning coffee.
3. Delivered expected insulin and then displayed the Eventual -456 mg/dl glucose level, shutting off the insulin.

Expected behavior Normal loop behavior.

Phone

• Hardware: iPhone 14 Pro Max
• OS Version: 16.2

Loop Version

• Version Number: v2.3.0 (57)
• Repo: Dev

CGM

• Device: Dexcom G6
• Manager app: Dexcom App

Pump

• Manufacturer: Insulet Pod
• Model: Dash
• Firmware version: 4.10.0 Export-20230101T113708Z.zip Export-20230101T125747Z.zip Loop Report 2023-01-01 063641-0500.md Loop Report 2023-01-01 075731-0500.md

Describe the bug I have a new iphone (mini 13, ios 16.2) and want to build my loop on it. I have previously used my old iphone SE. I build loop from my macbook air (Ventura 13.1) with the latest version of XCode (14.2). The build seems succesfull as xcode said running loop on iphone, and I didnt see any red bugs. When opening loop on my Iphone it did not show my old settings, the app seemed empty (I decided to first install everyting on my new Iphone before transfering my pods). After a few moments the app keeps crashing and shutting down. The first time it happend Xcode was still open and showed a popup messages saying "Terminated due to memory issue".

Attach an Issue Report Issue report attached and screenshot added. Loop Report 2022-12-29 08:14:26+01:00.md

To Reproduce Steps to reproduce the behavior: This happens each time I open Loop. Loop is also not open long enough to add settings

Expected behavior I hoped Loop would just open like before, maybe I had to add some settings, but I did not expect it to crash immediatly

A clear and concise description of what you expected to happen. I hope someone can tell me where I did something wrong so loop will work again :-)

Screenshots

Phone

• Hardware: [e.g. iPhone mini 13]
• OS Version: [e.g. iOS 16.2]

Loop Version

• Version Number: [V2.2.9]
• Repo:

CGM

• Device: [Dexcom G6]
• Manager app: [Dexcom App]

Pump

• Manufacturer: [omnipod]
• Model: [eros]
• Firmware version:

Additional context Add any other context about the problem here.

Is your feature request related to a problem? Please describe. The expiration for the new github Build Action process for building Loop does not notify user when Beta test will expire:

• The TestFlight distribution has an end date of 90 days
• The profile expiration might be a full year in the future (for first build with this method)

Describe the solution you'd like Add a new notification that warns user when app will expire - similar to the notification for Xcode built apps.

Additional context Is there a way to add the TestFlight expiration date to Loop notifications?

Testing Details The expiration profile for my TestFlight app reports as 2023-12-15 in the Loop Report under Build Details. I looked at:

• https://developer.apple.com/account/resources/profiles/list
• there are 6 profiles listed that start with match.AppStore.com for Loop through Loop Status Extension with that expiration date.

The TestFlight expiration says 87 days.

• Today is Dec 27, 2022.
• I changed the date (this is a test phone - do NOT do this on a real phone) to March 30, 2023 (93 days in the future).
• I can no longer open the app - message is: "Loop" Beta Has Expired
• Changed time to March 23, 2023 and app opens again

Hi, I tried to install the loop but in the final step I ran into a problem, I tried several times to install according to the instructions but it still doesn't work. Attach photos.

Is your feature request related to a problem? Please describe. There have been multiple posts on social media from Loop users who report difficulty understanding the effect on Loop predictions when they add carbs while running an override. The more extreme the override, the bigger the issue.

• The override properly affects basal rates, carb ratio and insulin sensitivity (because the ratio of ISF and CR is critical for predictions)
• However, sometimes people forget or do not understand the consequence of an override when entering or editing a carb entry.

Describe the solution you'd like One solution is to alert users that an override is in effect when a carb entry is entered or edited.

Describe alternatives you've considered There are a lot of posts on Facebook on this topic explaining what happened and why there is an unexpected bolus suggestion or unexpected prediction. It is covered in documentation, but even experts sometimes forget.